Playing with gganimate: Robust Estimation
Robust Estimation
OLS is not robust to outliers. It is computed by minimizing the sum of squares of the residuals and each outlying observation has a large residual and consequently a large effect on this sum of squares. On the other hand, The M-estimators used in robust statistics (Heritier et al. 2009; Huber 1964; Maronna, Martin, and Yohai 2006) are not influenced by outlying data. Huber (1964) proposed to minimize functions which are less influenced by outliers rather than the sum of squares. This functions are a central to the theory of robust statistics and are called
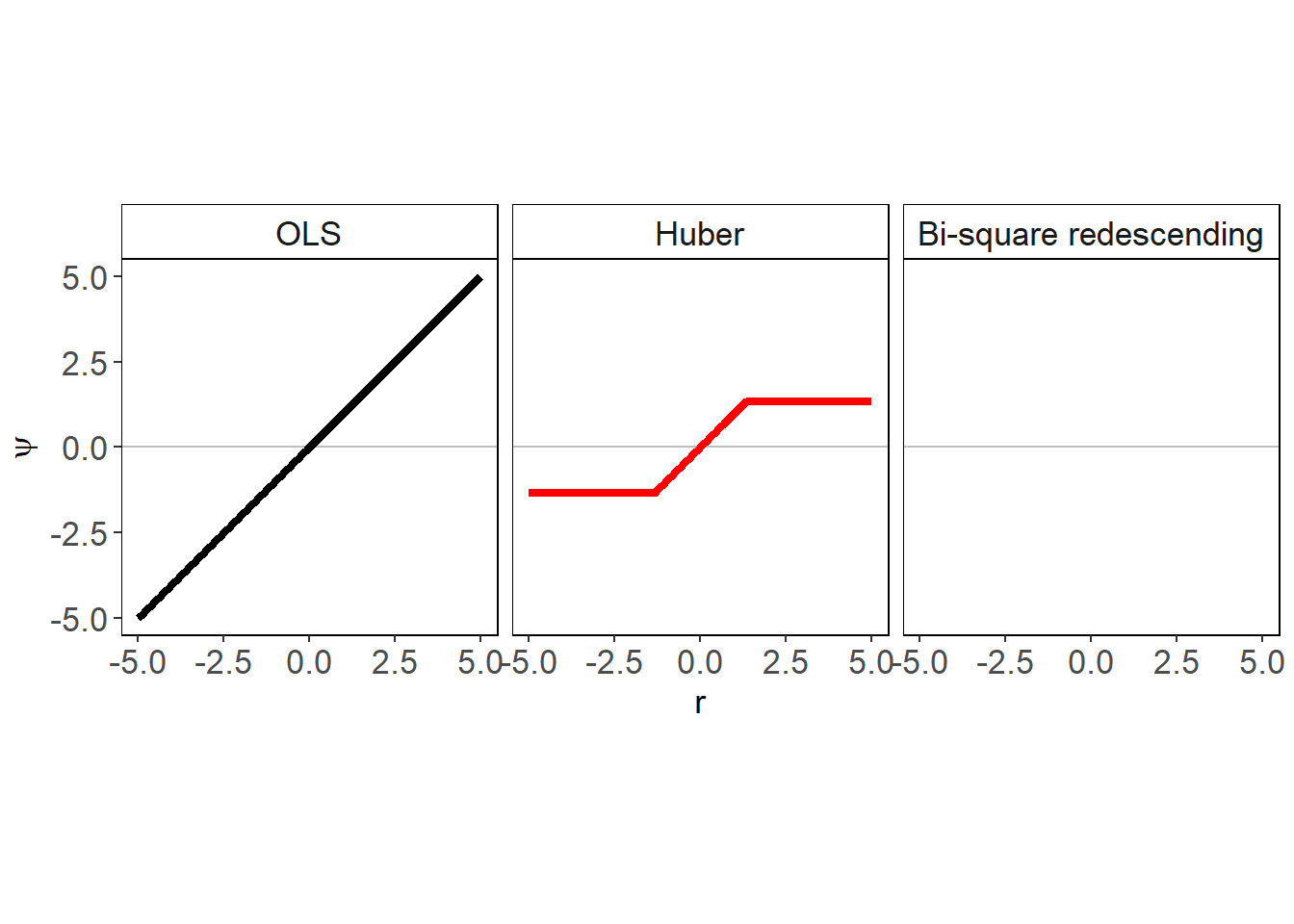
The OLS has a
Using R in regression, the rlm() function from the MASS package (Venables and Ripley 2013) computes the Huber estimator and the lmrob() function from the robustbase (Maechler et al. 2016) package uses the bi-square redescending
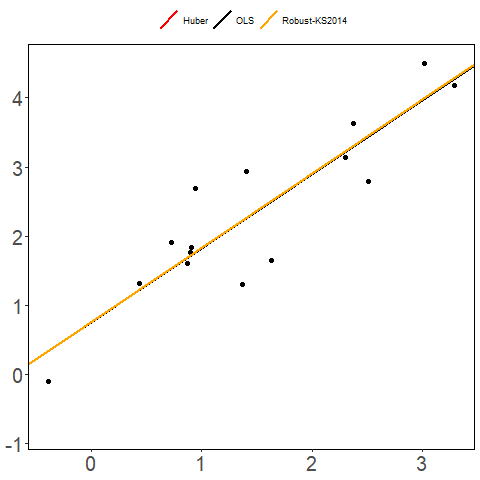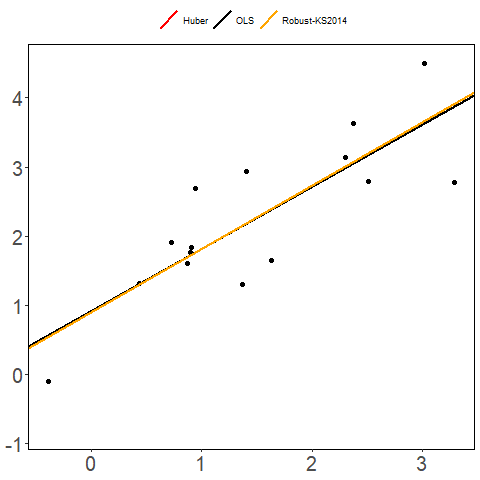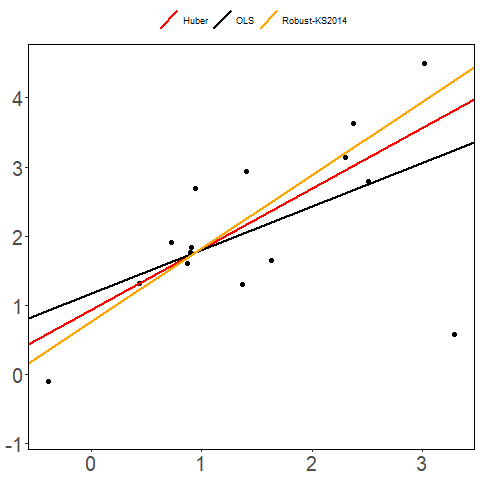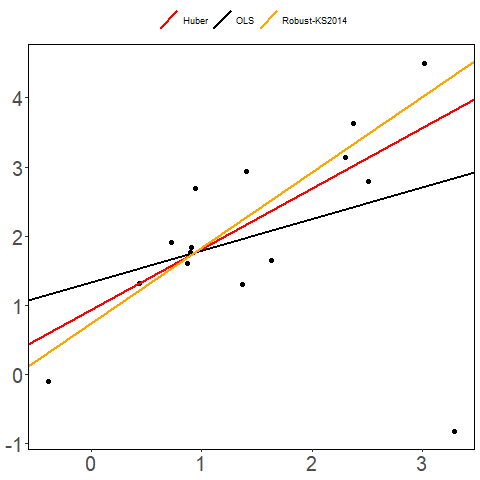
References
Heritier, Stephane, Eva Cantoni, Samuel Copt, and Maria-Pia Victoria-Feser. 2009. Robust Methods in Biostatistics. John Wiley & Sons.
Huber, Peter. 1964. “Robust Estimation of Location Parameter.” The Annals of Mathematical Statistics 35 (1): 73–101.
Koller, Manuel, and Werner A. Stahel. 2011. “Sharpening Wald-Type Inference in Robust Regression for Small Samples.” Computational Statistics & Data Analysis 55 (8): 2504–15. https://doi.org/10.1016/j.csda.2011.02.014.
Maechler, Martin, Peter Rousseeuw, Christophe Croux, Valentin Todorov, Andreas Ruckstuhl, Matias Salibian-Barrera, Tobias Verbeke, Manuel Koller, Eduardo L. T. Conceicao, and Maria Anna di Palma. 2016. “Robustbase: Basic Robust Statistics.”
Maronna, Ricardo, Douglas Martin, and Victor Yohai. 2006. Robust Statisics : Theory and Methods.
Pedersen, Thomas Lin, David Robinson, and RStudio. 2019. “Gganimate: A Grammar of Animated Graphics.”
Venables, William N., and Brian D. Ripley. 2013. Modern Applied Statistics with S-PLUS. Springer Science & Business Media.